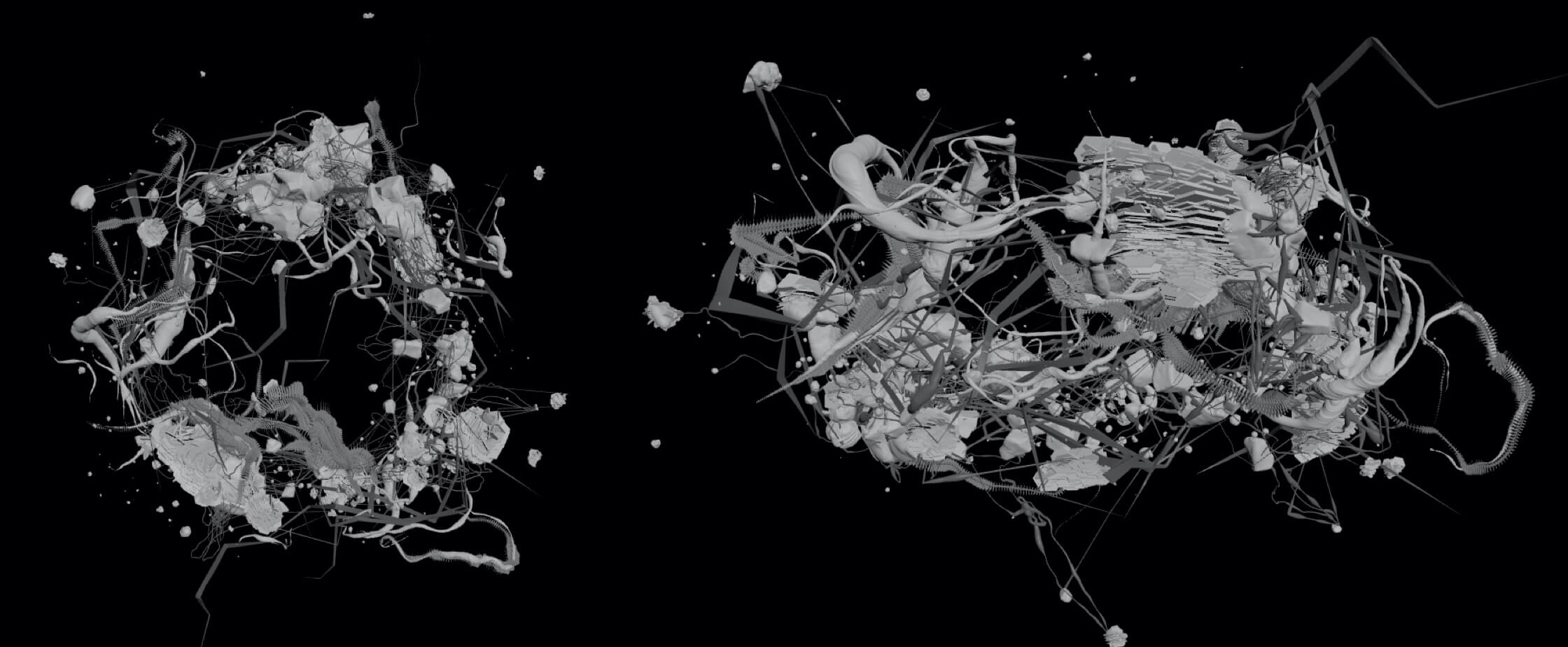
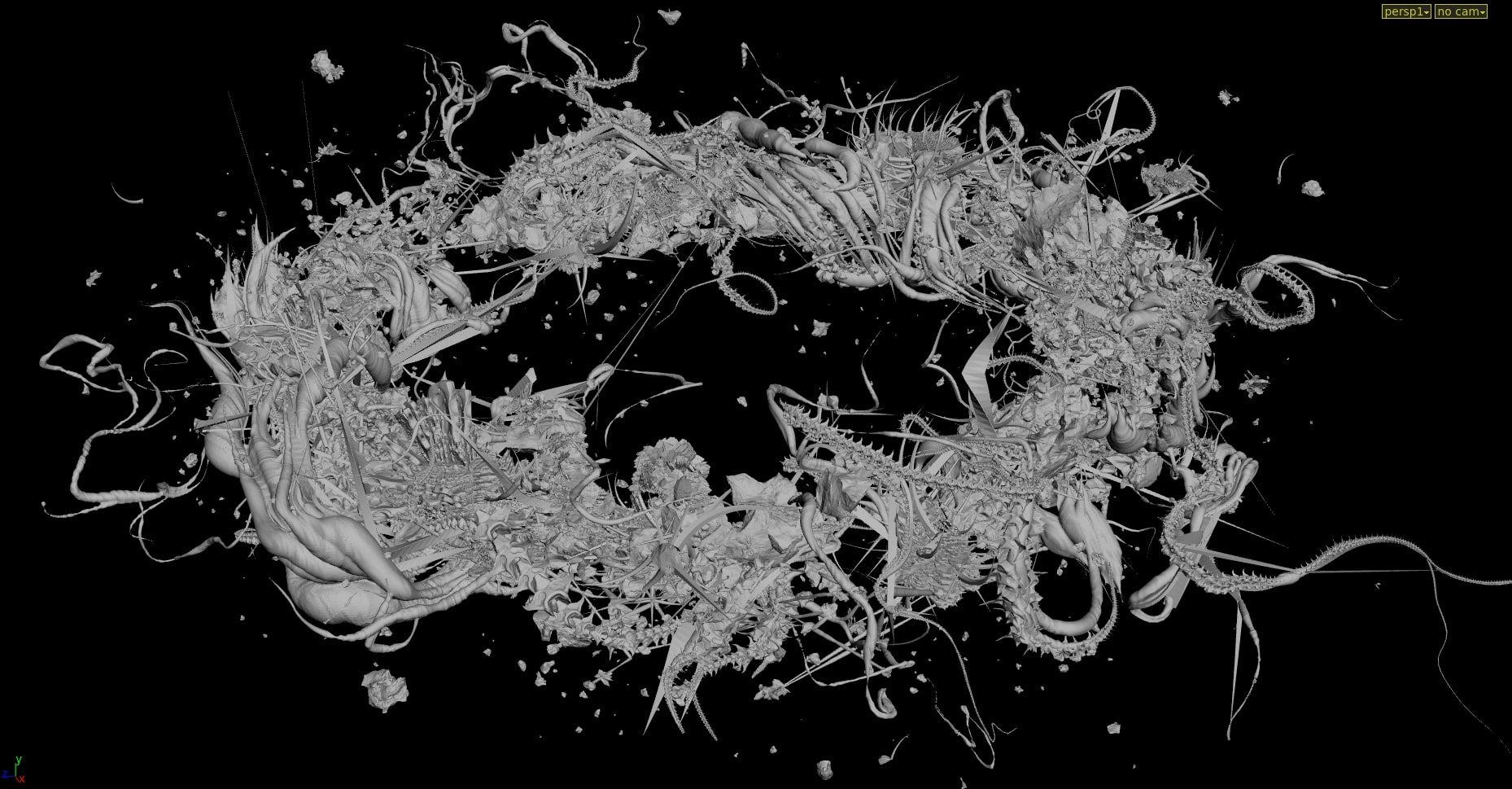
↪︎Rorschach happened to be the very first asset created for this film. A ship-organism, combining the properties of living matter and machine—what algorithmic modeling objective could be more fascinating? We started preliminary testing, but after some calculations it became apparent that the object’s shape was not quite what we had envisioned.
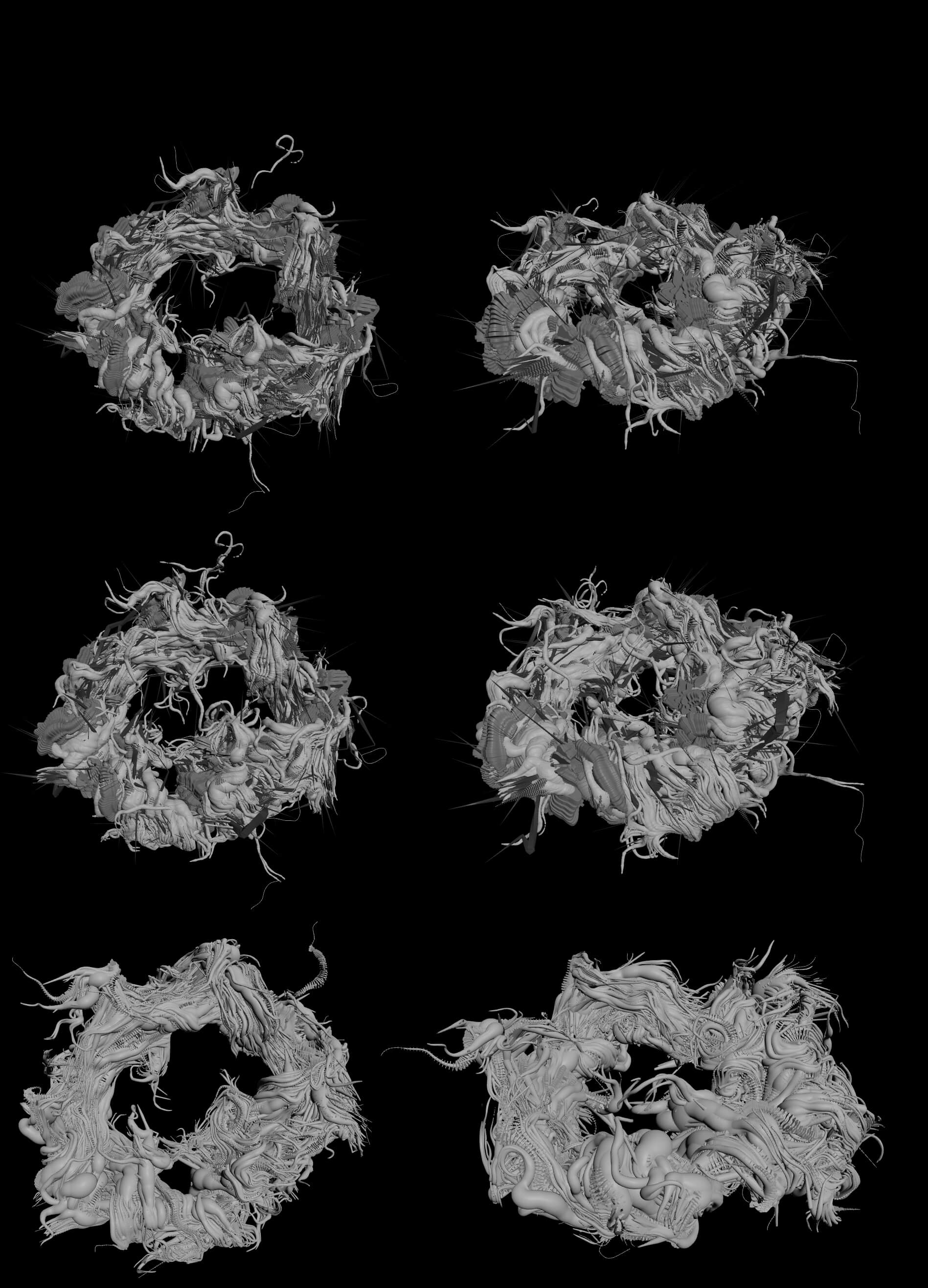
↪︎Based off the book, we’d imagined rorschach as a very massive torus (with all those spikes and spines on top), but then the math kicked in. We got the torus radius (15000 meters) and volume from these references: "this thing hiding in the shadow of ten jupiters was almost 30 kilometers from side to side." and " rorschach massed 1.8.10^10 kg within a total volume of 2.3.10^8 cubic meters." From the torus volume formula we were able to calculate the radius of the "tube" forming it. We were surprised to discover that the radius was only 28 meters - more like a "very slim, 30 km-diameter ring" rather than a "massive torus-shaped city”.
↪︎We realize that it’s not a perfectly-shaped torus, but we were thinking we could probably still use this formula. But judging by the details mentioned in the book, we had been expecting the ring’s inner radius to be around 3-5 km. The question is, was this the way you imagined rorschach? As a very slim ring with a huge diameter, but comparatively tiny inner tube radius?
↪︎Actually, I never envisioned Rorschach as a single integrated structure—more as a toroidal cloud of objects, loosely connected and held together by magnetic fields:
...the overall outline was that of a torus, or perhaps a collection of smaller jagged things piled together in a rough ring...
So most of that volume is empty space. But looking back, I guess I didn't reinforce that point after they started getting detailed telemetry, so I can see how you'd think it was a single massive object.
↪︎I must've based that mass on something—I don't think I'd pull such a number out of my ass without doing a few back-of-the-napkin calculations first— but offhand I doubt I saved them. I guess I never thought anyone would check. But purely backpedaling, I'm guessing the difference is that your calculations assume a solid contiguous structure and mine assumed a cloud.
At least, I hope that's it.
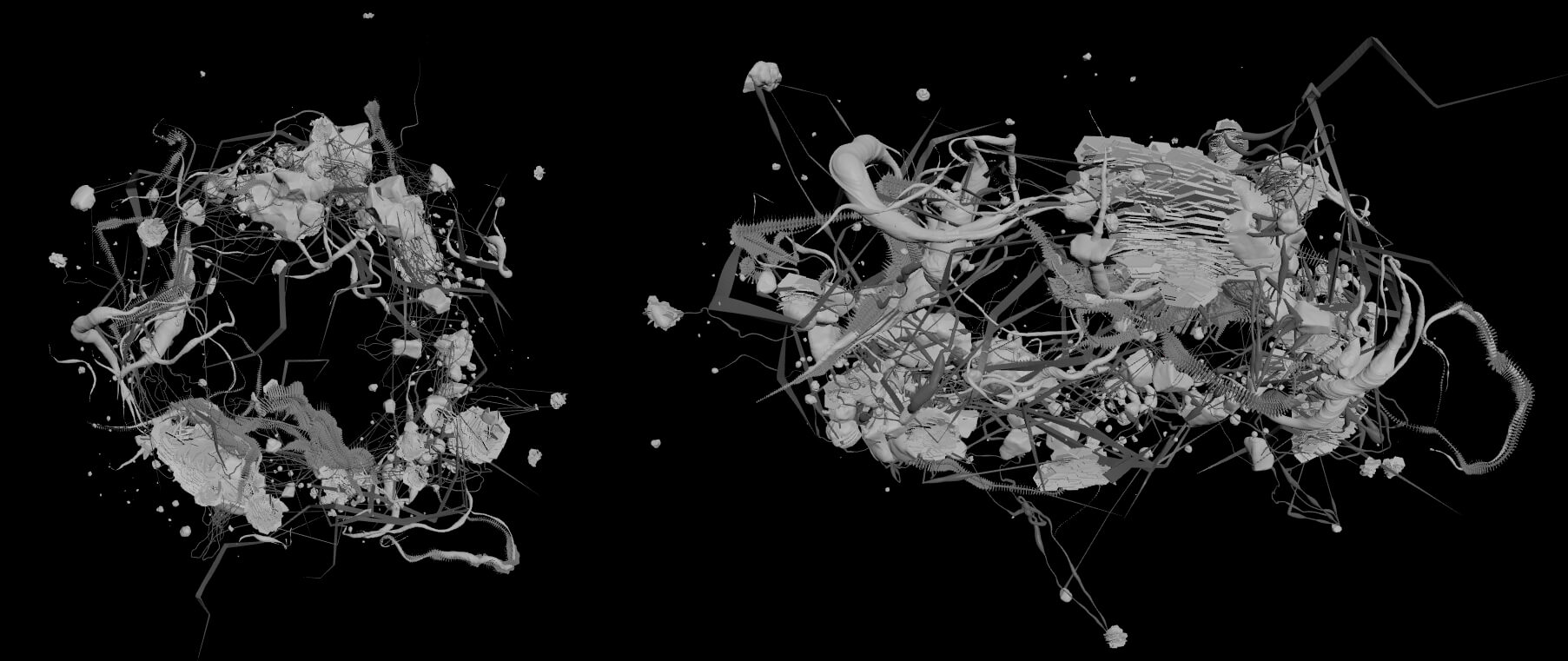
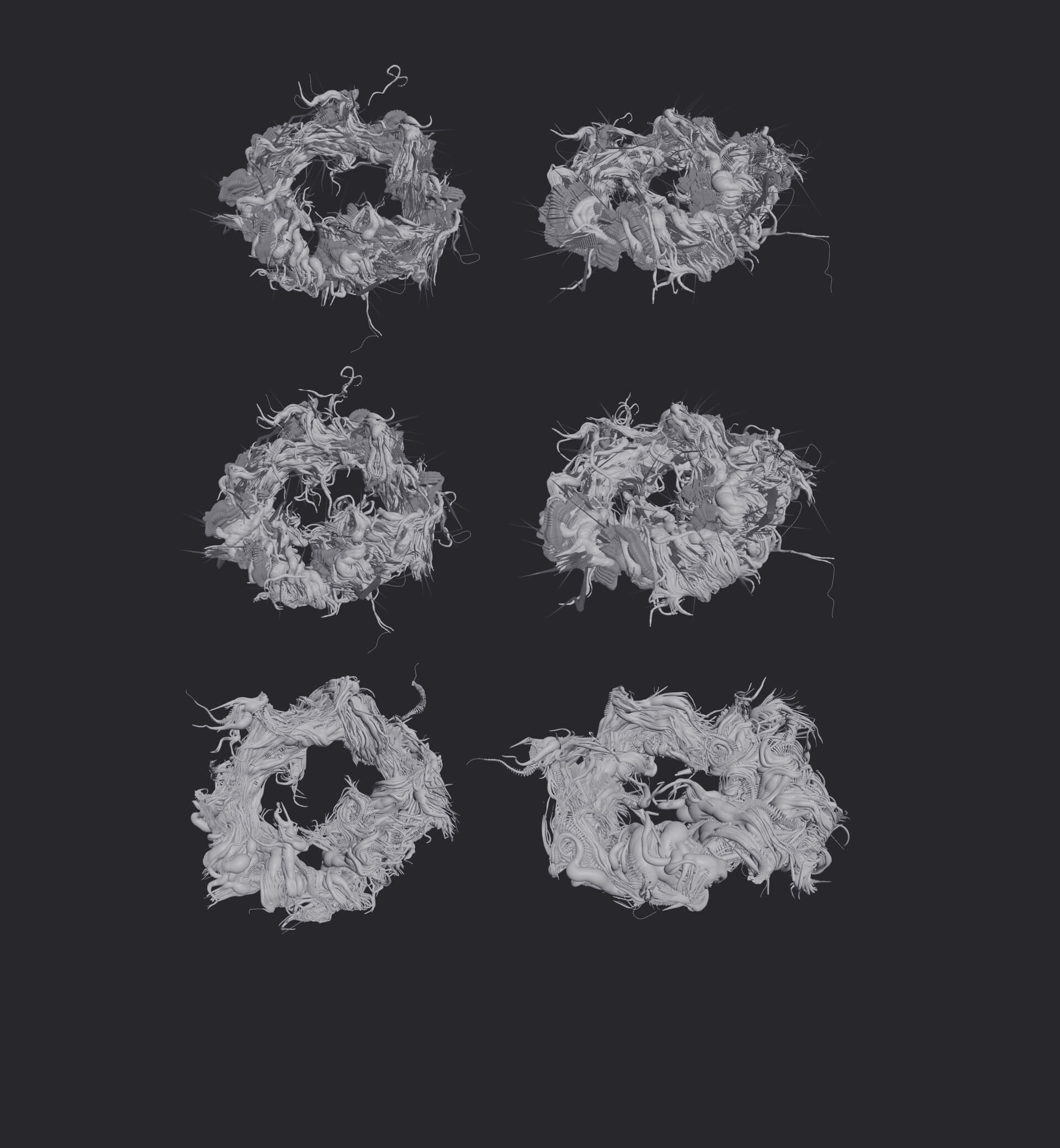
↪︎With your input, i now see that it should look more like this. Did i get it right? And by the way, which version is more accurate, a or b?

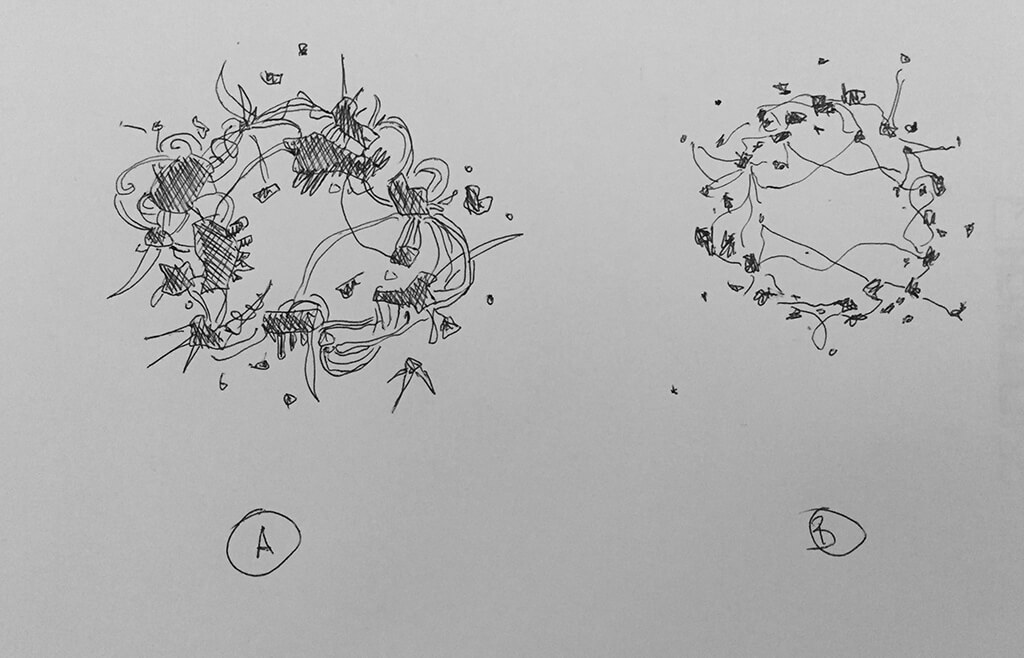
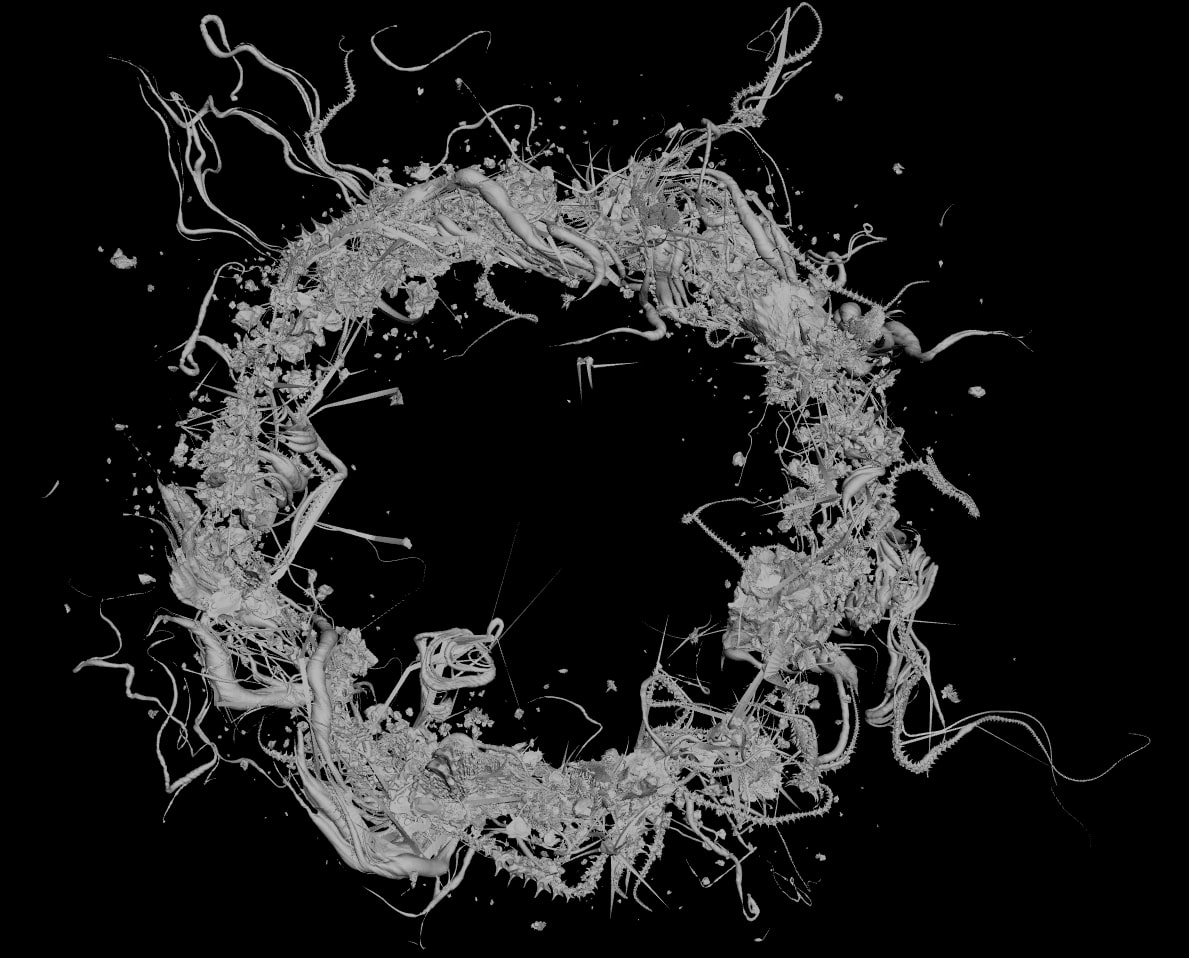
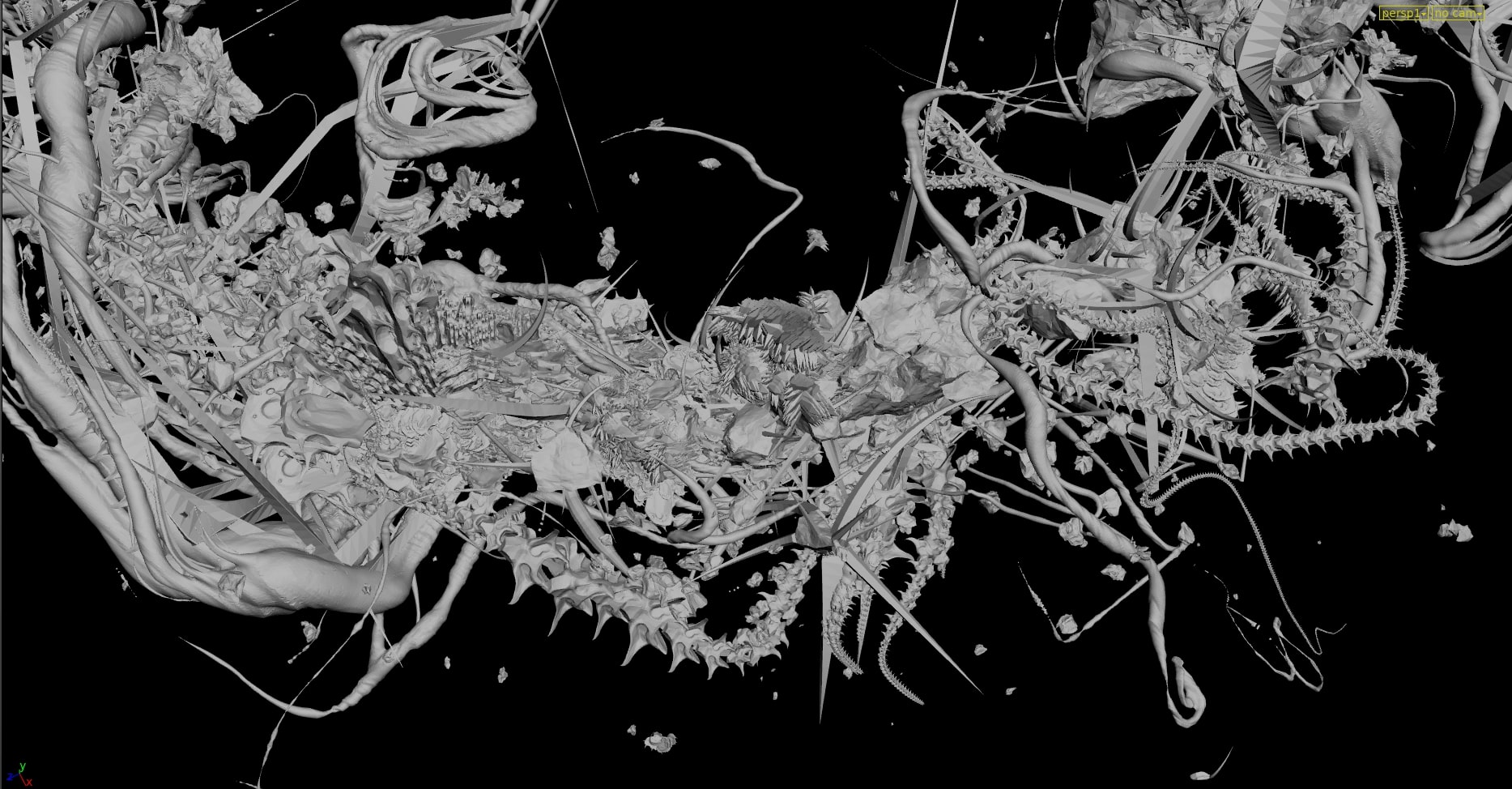
↪︎B, really. The chunks are held together by spines and spires and magnetic fields, so they're jumbled pretty closely together. Actually, the art that comes closest to portraying the fragment-density i had in mind was this chinese cover from a few years back; i imagined a thinner torus (bigger hole in the middle), but it captures the overall sense of jostling pieces in close proximity.



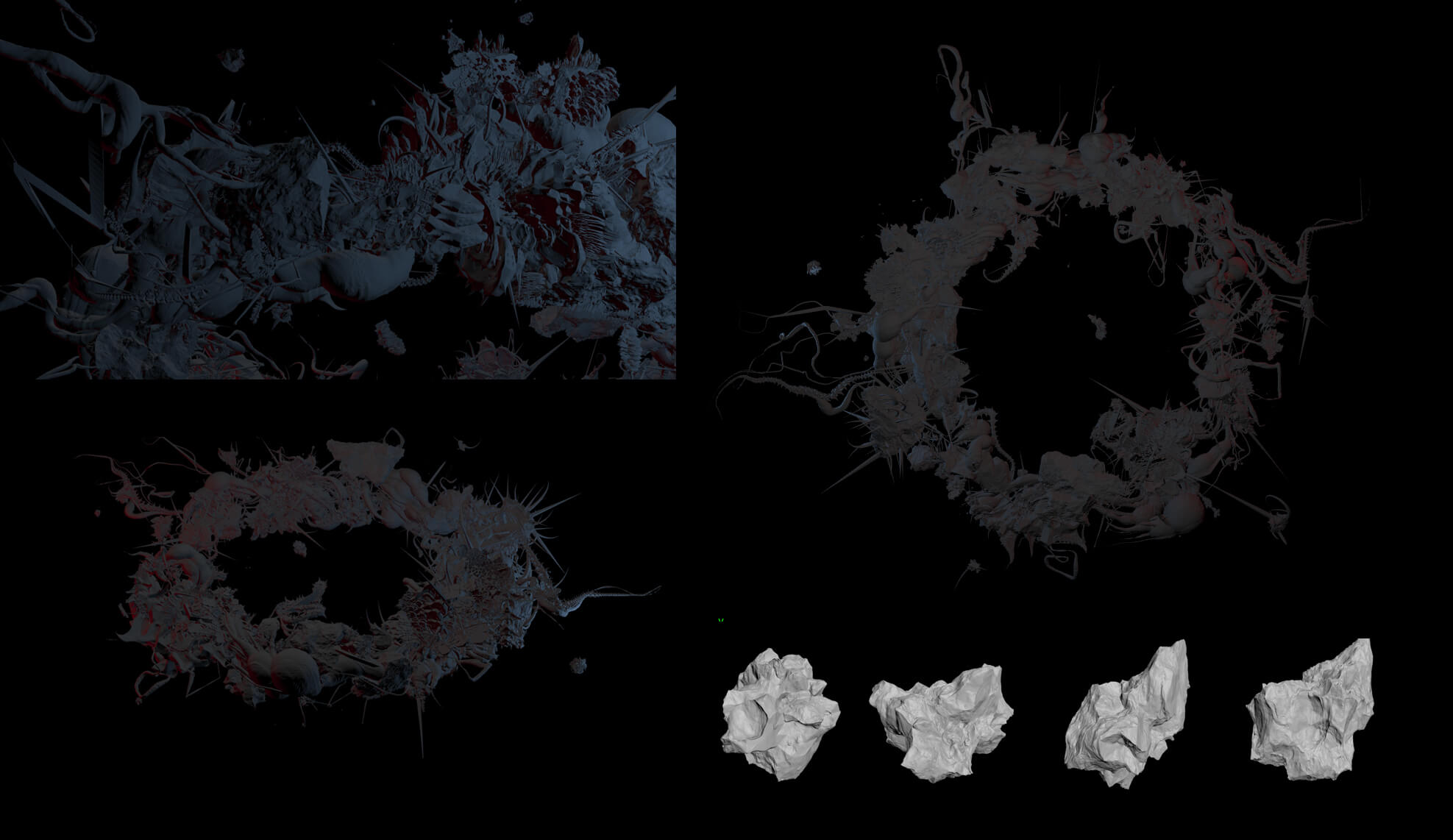


↪︎Here’s a new take on Rorschach. Let us know what you think!


↪︎Dude, that's pretty amazing. Even in it's current rough state, it's by far the most atmospheric rendition of Rorschach I've seen, in terms of conveying the image that was in my head when I was writing the book…
…The only complaint I'd have is the scale of the individual components is too large relative to the scale of the overall megastructure. All those loops and jags and rocky outcrops should be more the size of the individual thorns in the Chinese illustration; Rorschach consists of thousands of those things.
Other than that, though, it's just about perfect.



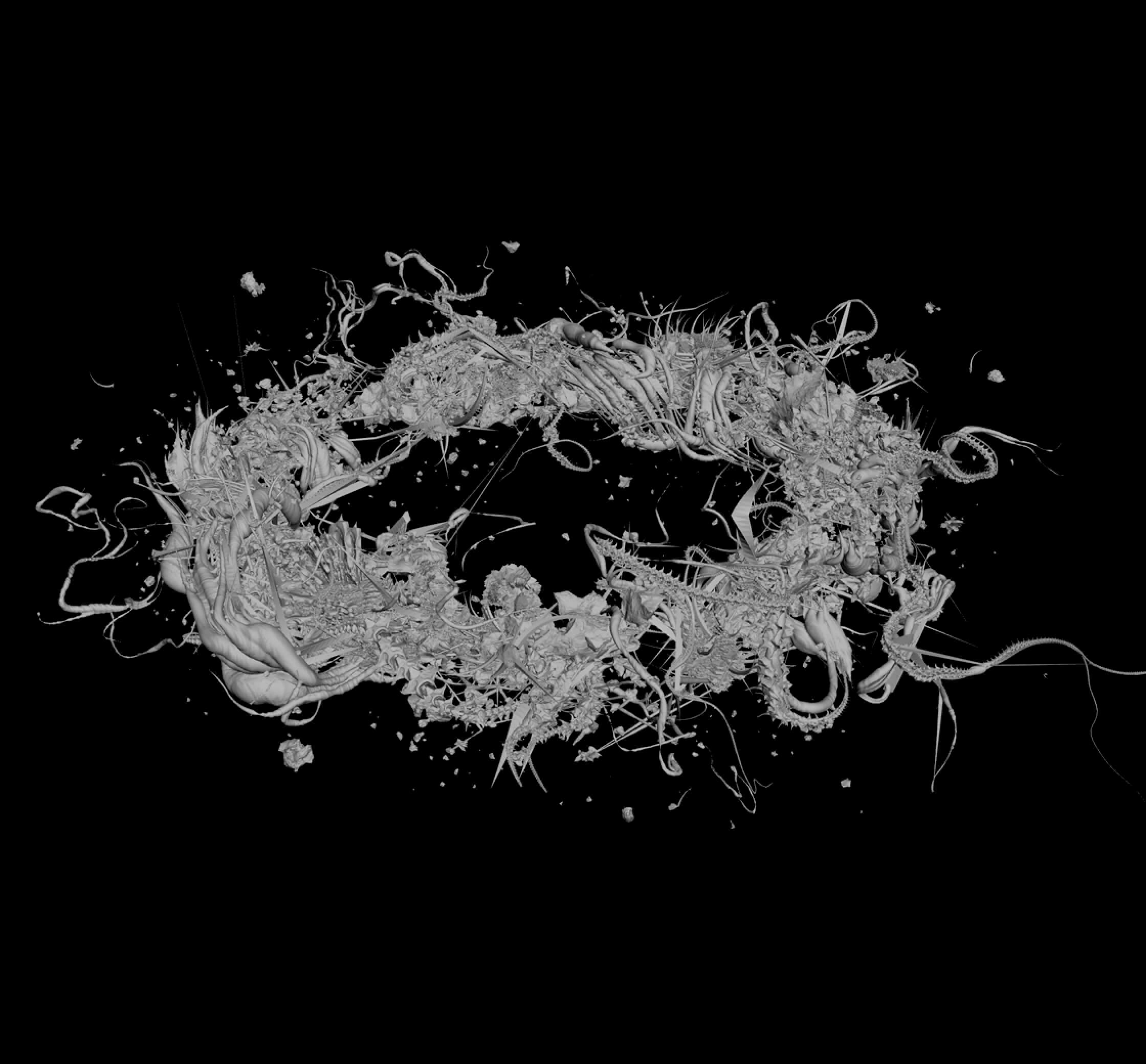
↪︎We are nearly done with the look and feel for Rorschach.
It’s time to start working on materials, shaders and all the final details for it.



-
Number of people involved:1
-
Hours Spent:340